棋牌游戏大厅开户

您现在的位置： 网上现金棋牌游戏平台 >> 棋牌技巧 >> 赌博游戏 >> 正文

从赌徒问题谈统计推测之重要性

分享到：
时间：2011-7-16
内容简介：首先我们来回顾赌博的起源，早在1600B.C.于埃及以及1300B.C.于中国均有关于赌博游戏之记载。尔后在十七世纪，法国贵族社会流行以投骰子作赌博，于投骰子中，反覆投几回后经验觉得有些结果不太一样。因此对当时之哲学者又是数学者间物理学者之 Pascal 及 Fermat 提出质疑且请求解释。于是这些学者乃开创了机率之概念且解出种种的赌博问题。在同时期 Huygens 之着作《骰子赌博之理论》以及 Jakob Bernoulli 之着作《推论法》等书均涉及机率理论之讨论。到 Laplace（1749-1827）时完成古典机率论。 本文由网上现金棋牌游戏平台www.crjq8.com编辑整理,介绍各种网上真钱棋牌游戏技巧,澳门赌场赌博技巧,提供各种网上博彩游戏,网上真钱游戏,免费试玩。希望从赌徒问题谈统计推测之重要性这篇文章能给你提供帮助。

棋牌游戏精简版下载 棋牌游戏完整版大厅下载

首先我们来回顾赌博的起源，早在1600B.C.于埃及以及1300B.C.于中国均有关于赌博游戏之记载。尔后在十七世纪，法国贵族社会流行以投骰子作赌博，于投骰子中，反覆投几回后经验觉得有些结果不太一样。因此对当时之哲学者又是数学者间物理学者之 Pascal 及 Fermat 提出质疑且请求解释。于是这些学者乃开创了机率之概念且解出种种的赌博问题。在同时期 Huygens 之着作《骰子赌博之理论》以及 Jakob Bernoulli 之着作《推论法》等书均涉及机率理论之讨论。到 Laplace（1749-1827）时完成古典机率论。

现在我们考虑下列一个赌博问题「今有一个圆铜板（不一定公正），设正面及反面发生之机率各为 $p,q(=1-p),0\leq p\leq 1$。今有一赌徒持有资金 a 元，而以金额 b 元赌「正面发生」，若猜中时，庄家赔 b 元，若未猜中则庄家赢 b 元（即赌徒输 b 元），如此继续打赌但每回打赌之金额不得超过该回赌博前之持有金额。设 N 回后，赌徒之财产为 ZN 时对赌徒之效用 (utility) 註1 为 $u(Z_N) = \log Z_n$（以 e 作底）。求使此期望值为最大之赌博政策（即 N 回之每回最适打赌金额）？」

此问题属于动态计画之问题，可利用最适性原理如下解此问题。此问题是由初期财产 a 元及计画期间 N 回（以 (a,N) 表示此问题），求出每回採用之最适打赌金额，及其最大利益 fN(a)，因此若初期财产为 x 元，没有打赌（期间0）时之最大利益为 $ f_0(x)=u(x)=\log x$ （因由题意赌徒财产 x 元时期效用为 $U(x)=\log x$）。

第一次打赌金额b元， $ 0 \leq b\leq a $ 时投出圆铜板结果，设其持有财产由 a 元变为 T(a,b) 元，T(a,b) 为如下：

\begin{displaymath} T(a,b)=\left\{ \begin{array}{l} a+b\mbox{, {\fontfamily{cwM1... ...cwM1}\fontseries{m}\selectfont \char 222})} \end{array}\right. \end{displaymath}

第一回打赌后赌徒持有财产为 T(a,b)，此为第二回至第 N 回之 N-1 回期间之初期财产，故对此问题 (T(a,n),N-1) 之最大利益为 fN-1(T(a,b))，因为 T(a,b) 有两种情形（正、反面）各以机率 p,q 发生，故第一回打赌 b 元后第二回到第 N 回之 N-1 回期间之最大利益期望值为 pfN-1(a+b)+qfN-1(a-b)。因此对问题 (a,N) 之第一回打赌金额 b 决定使 pfN-1(a+b)+qfN-1(a-b) 之值最大者，如此可得下列式（最适性原理）

\begin{displaymath} f_N(a)=\max_{0\leq b\leq a}[pf_{N-1}(a+b)+qf_{N-1}(a-b)] , \quad N=1,2,3,\cdots \eqno{(1)} \end{displaymath}

如上述使(1)是成立之 b 为问题 (a,N) 之第一回打赌的最适金额，但无法直接由(1)式求出，可利用(1)之递迴关系式如下解之。下列分为两种情形考虑。

(A) $p>\frac{1}{2}$ 时，由 N=1 开始，解出问题 (x,1)，即初期持有财产为 x 元只打赌一回，求第一回之最适打赌金额及函数 f1(x)。因为(1)式 a 改为 x，N=1 亦成立且 $f_0(x)=\log x$，故下式成立

\begin{eqnarray*} f_1(x)&=&\max_{0\leq b\leq x}[pf_{0}(x+b)+qf_{0}(x-b)]\\ &=&\max_{0\leq b\leq x}[p\log(x+b)+q\log(x-b)] \end{eqnarray*}


利用微分

\begin{displaymath} \frac d{db}[p\log(x+b)+q\log(x-b)]=\frac p{x+b}-\frac q{x-b}=0 \end{displaymath}

可求得 b 值（设为 b1*(x)）及 f1(x) 如下：

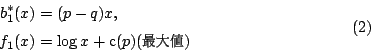
\begin{displaymath} \begin{eqalign} b_1^*(x) &= (p-q)x, \\ f_1(x) &= \log x + \... ...}\fontseries{m}\selectfont \char 77})} \end{eqalign}\eqno{(2)} \end{displaymath}

在此 $\mbox{c}(p) = p\log{2p} + q\log{2q}$。

其次考虑问题 (x,2)，即在(1)式中 a=x, N=2 及由(2)可得

\begin{eqnarray*} f_2(x)&=&\max_{0\leq b\leq x}[pf_1(x+b)+qf_1(x-b)]\\ &=&\max_{0\leq b\leq x}[p\log(x+b)+q\log(x-b)+c(p)] \end{eqnarray*}


如上利用微分，可求得 b 值（设为 b2*(x)）及 f2(x) 如下：

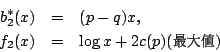
\begin{eqnarray*} b_2^*(x)&=&(p-q)x,\\ f_2(x)&=&\log{x}+2c(p)(\mbox{{\fontfamil... ...inus0.1pt{\fontfamily{cwM3}\fontseries{m}\selectfont \char 77}}) \end{eqnarray*}


如此由归纳法，对问题 (x,n) 可得

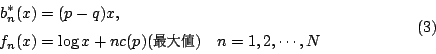
\begin{displaymath} \begin{eqalign} b_n^*(x) &= (p-q)x, \\ f_n(x) &= \log x+nc(... ...tfont \char 77})} \quad n=1,2,\cdots,N \end{eqalign}\eqno{(3)} \end{displaymath}

即

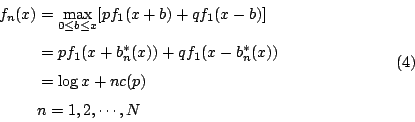
\begin{displaymath} \begin{eqalign} f_n(x) &= \max_{0\leq b\leq x}[pf_1(x+b)+qf_... ... &= \log x+nc(p)\\ & n=1,2,\cdots,N \end{eqalign}\eqno{(4)} \end{displaymath}

利用(3),(4)式可得问题 (a,N) 之最适赌博政策如下。

若 $p>\frac{1}{2}$ 时，设 b10=bN*(a)=(p-q)a，由(4)可得

\begin{eqnarray*} f_N(a)&=&\max_{0\leq b\leq x}[pf_{N-1}(a+b)+qf_{N-1}(a-b)]\\ &=&pf_{N-1}(a+b_1^0)+qf_{N-1}(a-b_1^0)\\ &=&\log a +Nc(p) \end{eqnarray*}

[1] [2] 下一页


来源：网上现金棋牌游戏平台
你可能感兴趣的：
没有相关文章
我们向您推荐的：
麻将经验
图说棋牌技巧
赌博游戏

双扣技巧
棋牌游戏下载
棋牌深海捕鱼

深海捕鱼

普通文章[组图]万王宝藏366
普通文章玩捕鱼游戏的好处1268
普通文章[图文]捕鱼游戏机单网技巧1198
普通文章[图文]金蟾捕鱼大揭密3701
普通文章[图文]大圣闹海2637
普通文章[组图]捕鱼达人2安卓破解版4249
普通文章[组图]波克城市新版捕鱼达人7336
推荐文章捕鱼游戏机赢钱技巧49653
普通文章[组图]捕鱼达人2全面介绍6083
普通文章qq捕鱼达人技巧3868

游戏视频


36棋牌深海捕鱼视频
36棋牌百变双扣

36棋牌斗地主
36棋牌红五三打一

经验分享

普通文章挖花唱词热点文章293
普通文章挖花怎么玩热点文章514
普通文章连连看必胜攻略热点文章496
普通文章打牌的原则热点文章1258
普通文章网上玩双升的技巧热点文章602
普通文章最全双升技巧热点文章938
普通文章打牌如何观察人热点文章3710
普通文章适合收藏的扑克品种热点文章691
普通文章扑克收藏的误区热点文章355
普通文章记忆提高创造力热点文章880

棋牌游戏攻略

推荐文章手部动作背后的心理最新文章
推荐文章根据手势判断对手的牌（二）
推荐文章根据手势判断对手的牌（一）
推荐文章手臂收回与冻结
推荐文章打牌中手臂的秘密
推荐文章躯干伸展的动作
推荐文章打牌时躯干动作给你的信号
推荐文章打牌过程中关于躯干的常识（二）
推荐文章打牌过程中关于躯干的常识（一）
推荐文章打牌露出马脚是要付出代价的（二）

斗地主

·[经验心得]“斗地主”的天时、地利、人和
·[游戏资料]哈尔滨，老年人也成为网络游戏“
·[棋牌游戏攻略]武汉斗地主情结
·[棋牌游戏攻略]相亲斗地主被骗输钱
·[棋牌游戏攻略]父亲斗地主丢子，3岁儿机智回家
·[棋牌游戏攻略]智运会斗地主
2010-2013 © 网上现金棋牌游戏平台 版权所有
增值电信业务经营许可证：粤B2-20169873-8 文网文编号：粤网文[2016]789114-088号